The Lottery Ticket Hypothesis - Paper Recommendation
I wanted to highlight a recent paper I came across, which is also a nice follow-up to my earlier post on pruning neural networks:
- J Frankle and M Carbin (2018) The Lottery Ticket Hypothesis: Training Pruned Neural Networks
Many people working on network pruning observed that, starting from a wide network and pruning it, one obtains better performance than training the slim, pruned architecture from scratch (random initialization). This suggests that the added redundancy of an overly wide network is somehow useful in training.
In this paper, Frankle and Carbin present the lottery ticket hypothesis to explain these observations. According to the hypothesis, good performance results from lucky initialization of a subnetwork or subcomponent of the original network. Since fat networks have exponentially more component subnetworks, starting from a fatter network increases the effective number of lottery tickets, thereby increasing the chances of containing a winning ticket. According to this hypothesis, pruning effectively identifies the subcomponent which is the winning ticket.
It's important to note that good initialization is a somewhat underrated but extremely important component of SGD-based deep learning. Indeed, I often find that if you use non-trivial architectures, training is essentially stuck until you tweak the off-the-shelf initialization schemes so that it somehow starts to work.
To test the hypothesis the authors have designed a set of cool experiments. The experiments basically go like this:
- start from a fat network
- train it
- prune it
- take the resulting skinny network and reset weights to their initial values (they call this the winning ticket)
- train the winning ticket network
- as a control, reinitialize the weights of the winning ticket randomly, and train that
Here are some of the results from Figure 4.
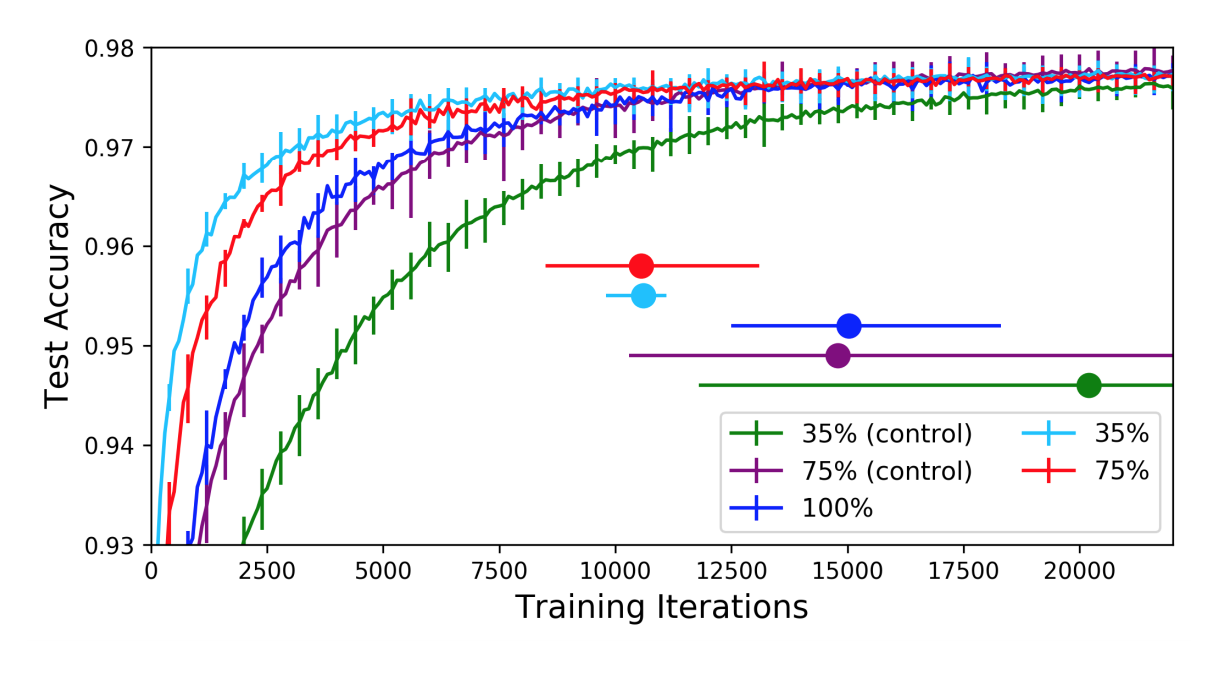
Observe two main things in these results. The winning tickets, without the remaining redundancy of the wide network, train faster than the wide network. In fact, the skinnier they are, the faster they train (within reason). However, if you reinitialize the networks' weights randomly (control), the resulting nets now train slower than full network. Therefore, pruning is not just about finding the right architecture, it's also about identifying the 'winning ticket', which is a particularly luckily initialized subcomponent of the network.
I thought this paper was pretty cool. It underscores the role that (random) initialization plays in successfull training of neural networks, and gives an interesting justification for why redundancy and over-parametrization might actually be a desirable property when combined with SGD from random init.
There are various ways this line of research can be extended and built upon. For a starter, it would be great to see how the results hold up when better pruning schemes and more general classes of initialization approaches are used. It would be interesting to see if the training+pruning method consistently identifies the same winning ticket, or if it finds different winning tickets each time. One could look at various properties of randomly sampled tickets and compare them to the winning tickets. For example, I would be very curious to see what these winning tickets look like on the information plane. Similarly, it would be great to find cheaper ways or heuristics to identify winning tickets without having to train and prune the fat network.
